 |
 Up
Up
|
|

|

|
Meet a Mathematical Inventor! |
|
|
|
|
|
|
Many scientists and engineers have attempted to create better calculating instruments in centuries past. Some are widely known: Newton, Pascal, Leibniz, Watt... some are well known to students of calculation history: Odhner, De Colmar, Thacher... and some are completely lost in obscurity – like Jean-Antoine Lafay. And yet M. Lafay turns out to be a fascinating innovator... even more interesting than his unusual calculator. Read on! |
|
|
|
The Hélice a Calcul |
|
|
|
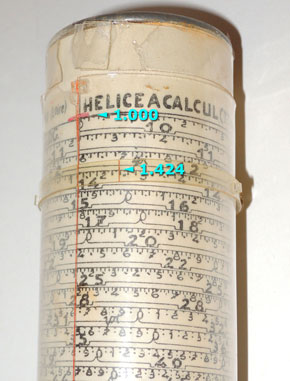
Lafay’s main contribution is the Hélice a
Calcul shown here. This is a novel variation on the helical slide
rule, better known in the earlier implementations of George Fuller
and of Otis King. Such a device always involves two elements: a very
long logarithmic scale that is wound tightly around a shorter
cylinder to achieve portability of the resultant calculator; and two
independently movable indicators that can point at two numbers on
the scale, then be moved as one to a new position to indicate a
result. Lafay’s device does this by placing the scale -- 2.5 meters long -- on a cardboard cylinder 19 cm long and 4 cm in diameter, and adding a transparent, movable cylindrical sheath, or sleeve, with one of the indicators marked as a red cross on its surface; the other indicator is a red hairline on a transparent movable cursor ring surrounding the sheath. My unit has two such movable cursors, one held tight with a rubber band and one without; you only need one of them to operate the device buy the instructions state that it was delivered with two spares. |
|
|
|
 Click photo to enlarge |
|
|
|
The next photo shows a close up of the indicators – A on the top of the sheath, and B on the cursor. It also shows three celluloid bumps -- tiny glued-on cubes -- one near the sheath’s indicator and two on the cursor flanking the red hairline. The latter give you a tactile cue to find the location of the indicator on the ring despite the visual clutter of the scale below. |
|
|
|
circular movement by hitting the bump just at the right starting position. This is clear from the drawing in the manual, and I found online here a photo of a Hélice a Calcul that clearly shows this feature. |
|
|
|
 |
|
|
|
Lafay’s manner of drawing the scale graduations is highly unusual. The graduations and numbers are below the line; to conserve space the two most significant digits are written in larger size at the bottom, and a horizontal curly brace shows the span these digits refer to; at the beginning of the scale, where the brace is longer, the two digits may be repeated a number of times. Above the brace appear numbers denoting the third significant digit, and the fourth digit |
|
|
|
We then move the sheath (leaving the cursor stationary with respect to it) to indicate 1832; the hairline on the cursor is now over 2609 -- a 4-significant-digit representation of the exact answer, 2.608768 (right photo). The decimal point’s location, as in all logarithmic slide rules, is left for the user to figure out. |
|
|
|
 Click a photo to enlarge |
|
|
|
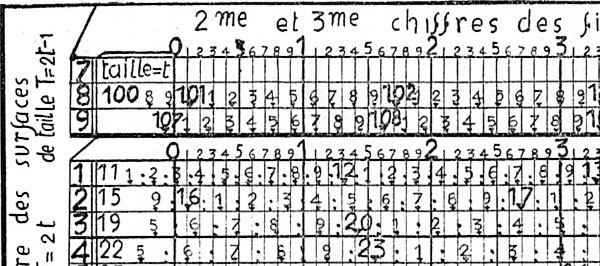
transparent wallet in which the tables could be made to slide
under a fixed reference line for rapid reference. He also devised
calendrical computing tools and published a method for representing
numbers “semi-logarithmically”, with the characteristic – i.e. order
of magnitude – separate from the significant digits: 62,350,000 is
written as (7) 6235, and 0.00023 as (-4) 23. The tables (with the exception of the multiplication table, which is ordinary) were just as quirky as the Hélice a Calcul’s scales, with the different digits spread all over the place. They were accurate and effective, but you had to learn to use them. Here is a representative one, for calculating the area of a circle; be sure to click it to see the entire table and its abstruse instructions of use. |
|
|
|
 Click photo to enlarge |
|
|
|
An enigmatic inventor So much for Lafay’s products; but as I said
before, the man himself turns out to be a very interesting fellow. |
|
|
|
The only correct claim Lafay makes is that his device is more
precise – with a 2.5 meter scale, it provides four digit accuracy
where a standard 30 cm linear slide rule gives three at most.
However, for 99% of an engineer’s or a scientist’s work three digits
are enough; it is no accident that Einstein, Teller and Von Braun
all used standard linear slipsticks. Moreover, if you needed higher
accuracy, you would probably get a Fuller or a Thacher slide rule,
or a mechanical Odhner type calculator, and charge the higher price
to your employer. This gap between Lafay’s opinion of his inventions
and the stark reality made me curious – was he some kind of deluded
“mad inventor”? Or an amateur dabbling in calculation aids?Meet the real Jean-Antoine LafaySo I decided to learn some more, and set out to read every word in the dozens of pages of instructions and brochures I’d received. Given the somewhat rusty state of my French, it took an effort – but it was well worth it. Hidden among the technical instructions and marketing copy were gems of personal narrative and opinionated rants, which expose a lot about the man’s thinking, methods and uneven career as an inventor. Here is my translation of some pertinent passages (originals can be found in the brochure and instructions). “[I was working on] a great table that, in 100 tabbed pages, would have directly given the products of the first 20,000 numbers by the 100 first ones, in less time than it would take to feed the data into a large calculating machine ... at a price very small compared to the machine’s. But in order to complete it I’d need the certainty of having at least 100 underwriters; only three have committed support. I therefore had to abandon this project, having already suffered too many losses with my other inventions”. “To help small merchants and accountants to make invoices containing tax calculations, I’ve produced on quality paper a few hundred copies of series of tables for fiscal calculations; it was a fiasco [I suspect that he uses Fiasco as a bitter word play on Fiscaux, fiscal –NZ]. The tables were rapidly made obsolete by changes in the taxes, and despite costly advertising and personal visits I could not convince more than a score of clients, admittedly enthusiastic but too few to allow me to continue to serve them, despite their insistent requests.” He then launches into this poetic diatribe: “Oh, routine! What wrong do you not do, firstly to your devotees who, to avoid a little effort of adapting to innovative tools and processes, which would render them remarkable service, are unwilling to budge from their old deplorable habits,... and then to these poor Don Quixotes who, in believing they might overcome them, only bruise themselves against your incredible force of inertia? And yet, poor fool that I am, with the present brochure I resume a battle that I should have abandoned, moved again by the illusion that I may end up victorious.” Get it? In my long career as an internal change agent in a large company, I have had to combat that inertia many times; I can feel for poor Jean-Antoine. And it isn’t only the prospective customers... he had even worse experiences with professors of mathematics. Here are a few snippets from a page-long tirade: “[I’ve managed to secure] a list of some 3,000 members of the association of mathematics professors. I’ve sent 800 of them my diverse documents, including that about factoring numbers; I got only one confirmation of receipt. Does the execrable routine strike even among professors?” “When I approached mathematics professors, they caused me great disappointment. ... their almost universal response was negative, formulated roughly thus: ‘the goal of our teaching is to develop the spirit and intelligence of our students, and your purely utilitarian mathematics are of no use for that; they are even harmful’.” A few professors were more accommodating, apparently: “Among those who had most encouraged and helped me I can mention M. Joseph Pérès, Dean of the Faculty of Sciences of Paris; MM. Jacob and Zadou-Naïsky, both associate professors of Physics, without whose support it would have been impossible for me to pursue my labors; and dear brother Antoine, of the Lazarist academy at Lyon, who ... had introduced me so warmly to the many mathematics students under his tutelage that these had entirely dispossessed me of the Hélices and Pochettes I had brought them, forcing me each time to make a second trip to content them all.” The cold reception by most professors notwithstanding, Lafay continues to reach out: “May I again ask Messieurs the professors of mathematics to get acquainted with this new method, then to authorize its use by their students, for whom the decomposition of numbers into their prime factors ... is purely a headache with no intellectual benefit whatsoever?” “I cannot continue [to send unsolicited materials], with so little result from spontaneous mailings, which are too expensive for my poor purse, but I will send for free my entire collection of instructions and tables to such professors as would ask me to do so.” “Unfortunately for the author, whose time is very limited, [the graphic tables] are extremely time-consuming to devise, and it would take him several years before he can publish the collection on which he is working. He would, in the meantime, receive with thanks critiques and advice that would help him make good this lengthy work. He apologizes for the poor legibility of the first tables; they were trial pieces, he will redo them.” And he also comes clean about his qualifications: “I take no part in teaching ... I am but a simple autodidacte, and only with great effort was I able to acquire the mathematical knowledge necessary for solving the problems I had to handle in my subsequent endeavors.” So now we know: Jean-Antoine Lafay was, indeed, an amateur. Working outside the educational and academic establishment, with but rare encouragement and few paying customers, he waged the battle of the lone inventor with tenacity and courage. I’ve met a number of his kind in my life, some more admirable than others, but all alike in their conviction that their idea is a great improvement on what everyone else is doing, if only they would open their eyes to see. To Lafay’s credit, his ideas may not have revolutionized science, or made him rich, but they do express great ingenuity. He successfully produced a long-scale slide rule at an amazingly low price point; his bizarre notations, scale arrangements, and “tableaux graphiques” are truly original, and full of interesting features. It is a pity he wasn’t born in the age of the Internet: he would have made a fine startup founder! |
|
|
|
Exhibit provenance: I purchased this item from a collector in France. More info: And here, Lafay's brochure describing his inventions (and tribulations). A
web page with
more information and photos of Lafay's products at the site |
|
|
|
|
|
|
|
Home | HOC | Fractals | Miscellany | About | Contact Copyright © 2017 N. Zeldes. All rights reserved. |
|





