The Fractal Bug

Home Up	Contact Legal Stuff

The Fractal Bug

Fractals never fail to fascinate. If you aren't just gazing at their unearthly beauty, you ponder the mathematics behind them... and then you can't help wondering how such simple math formulas can give rise to such intricacy. What is it about the fabric of the cosmos that makes it possible for a short, ugly equation to generate the exuberant beauty of the Mandelbrot set? Or is it all just in the way our brains are wired?

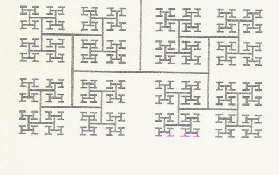
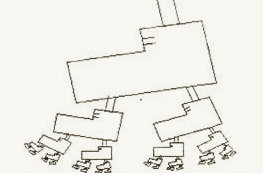
		My love affair with fractals started in 1985, when Scientific American magazine ran a cover story (reprinted here) on the Mandelbrot set. Gazing at this in print was fine as far as it went, but the thing to do was to generate it oneself, and in those days we had little access to the required computing power... but we sure tried. My coworker Amir mailed me a paper printout -- the one on the right -- with a Julia set he managed to render. For my part, at the time I was playing with the Logo language on my C-64, trying to teach it to my kids (accepted wisdom was that Logo is great for kids; but my own children evidently hadn't read that, for they grasped Logo rapidly, then dumped it in favor of Basic...) Logo was wonderfully suited to recursive routines, as well as to vector graphics, so I had a good time experimenting with fractals by doing recursive "turtle graphics"; you can see two examples of the outcome below.	$Amir's fractal$
		Fractals generated in Logo on the Commodore 64

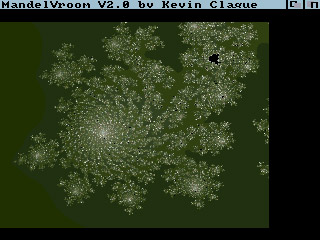
And then came the Commodore Amiga, that hacker's dream machine. Now I had the power to explore the Mandelbrot set. I used a number of public domain programs, notably MSE and MandelVroom. At right you see the achievable quality (this was stretched across an entire screen, mind you). At 320x200 and 32 colors, a far cry from today's tools -- but compared to the pictures seen above...
All this was slow work, for it could take an hour to render a single image like the one at the right, dot by dot. But it was worth it, if only for the suspense as the image emerged before one's eyes!

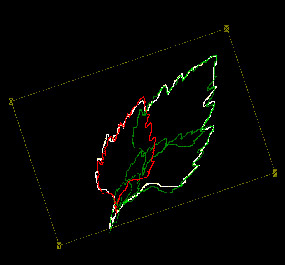
		The January 1988 issue of Byte magazine had an article on "A better way to compress images", by Barnsley and Sloan. This was my first glimpse of Iterated Function Systems, and of Barnsley's technique of tiling distorted small copies of an image to cover the original image precisely, thereby identifying the transformations that would serve to reconstruct the image later. When I read that, and saw the figure reproduced below (left), I immediately knew I wanted to play with this "Collage theorem" directly! It was so obviously going to be fun, using a mouse-driven interface to move, stretch and distort the copies of the fractal that create the Collage and see the effect on the attractor. To my surprise, none of the IFS programs I've seen in the public domain ever allowed that (they'd all represent the transformations schematically with triangles or rectangles, never with the actual image). So I knew I'd have to do something about that myself. It took years, but I did; the article's leaf collage that had triggered my interest, generated in my very own program, is shown below at the right.
		Click a photo to enlarge
		That program was IFS Lab, a tool for generating fractals using the Collage Theorem, whose latest version is available for download on this web site. The original version was written in C on the Commodore Amiga, a project which I finished in 1992; the Amiga was eminently suited to Graphics wizardry, but I wasn't... and I'd never written a program of this size before. The result was shared in the Fred Fish PD library, on disk 696 (that's floppy disk 696... in those pre-web days freeware was distributed on physical media). Then the Amiga era ended, and I moved my hobby to the IBM PC... and I missed my Collage fun. So in 1998 I decided to port IFS Lab, this time in C++ (I didn't know C++, so here was my opportunity to learn it). The outcome, 7 years later, was more than a port; it is faster, more flexible, and with better graphics than the original. The basic user interface is the same, though -- no need to mess with a good thing... You can see the two programs' screenshots here -- similar indeed, but you can see the progress the industry has delivered in screen resolution and user interface "look and feel" in the course of a mere dozen years. So what do I do now that IFS Lab is released? Well, I have some time at last to attend to the other programming projects on my list -- and in the coffee breaks I can always try to create ever more lovely IFS's... or use the superior programs that have come out over the years (my favorite is Fractal eXtreme) to explore the Mandelbrot set in all its glory. Isn't it breathtaking?